بهینه‌سازی مسائل چندهدفه

مسئله بهینه‌سازی

مسائل بهینه‌سازی جندهدفه داری بیش از یک تابع هدف هستند ممکن است برخی از آن‌ها بیشینه‌سازی و برخی دیگر کمینه‌سازی باشند. برمبنای همه‌ی آن‌ها کیفیت راه حل‌های ممکن را ارزیابی می‌کنند. به عبارت دیگر موقعیتی از فضای جست‌و‌جو که در آن تمامی توابع هدف بهینه باشند، تعیین می‌شود.

اگر تمامی توابع هدف از یک جنس باشند، یعنی متغیرهای یکسان یا همجنس داشته باشند، آن مسئله، مسئله‌‌ بهینه‌سازی چند هدفه نیست! تمامی توابع هدف آن باید در یک تابع هدف وارد شوند و به آن به دید مسئله بهینه‌سازی تک‌هدفه نگاه کرد.

مفهوم موقعیت بهینه در مسائل بهینه‌سازی با چند تابع هدف متفاوت از مسائل بهینه‌سازی تک‌هدفه است.

به‌طوری که دو اصطلاح جدید، جواب مغلوب و نامغلوب مطرح می‌شوند.

در مسائل چند هدفه در فضای جواب اگر حداقل یک تابع هدف نقطه A بهتر از حداقل یک تابع هدف نقطه B و باقی توابع هدف دو نقطه برابر باشند، بدیهی است که نقطه A برتر از نقطه B است و در نتیحه نقطه B توسط نقطه A مغلوب شده است؛ اما اگر تابع هدف f در نقطه A بهتر از  نقطه B باشد و تابع هدف z در نقطه B بهتر از نقطه A باشد و باقی توابع هدف با هم برابر باشند، بین نقطه A و B برتری وجود ندارد و در نتیجه دو نقطه A و B نامغلوب هستند.

در مسائل چند هدفه، ما همواره به دنبال مجموعه ای از نقاط نامغلوب برتر هستیم که به آن پارتو فرانت می‌گویند. از آنچایی که پارتو فرانت مسئله معمولاً شامل چندین جواب است، مسائل چندهدفه روش حل دقیقی ندارند. روش حل این مسائل به دو دسته سنتی و مدرن تقسیم می‌شوند.

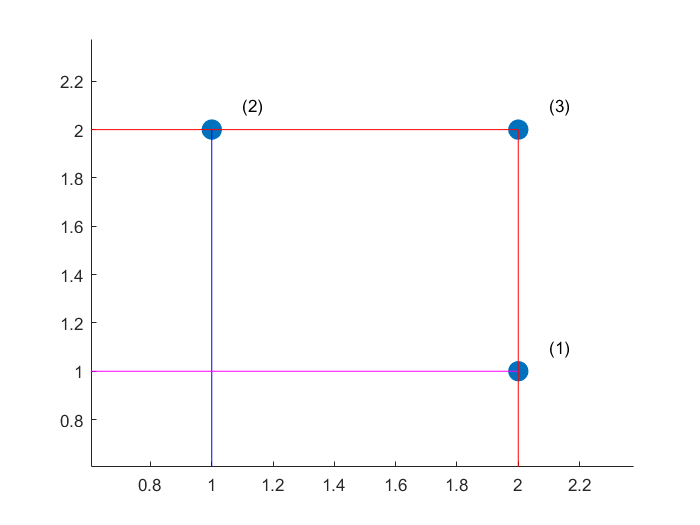
به شکل زیر توجه کنید. هدف مسئله کمینه‌سازی f(x) و g(x) است. 3 جواب متفاوت در فضای جواب مسئله یافت شده است.

نقطه (1) با مقادیر f(x)=1 و g(x)=2، نقطه (2) با مقادیر f(x)=2 و g(x)=1 و نقطه (3) با مقادیر f(x)=2 و g(x)=2 بدست آمده‌اند.

مقادیر توابع هدف نقطه (3) بیشتر از مقادیر توابع هدف نقاط (1) و (2) هستند، در نتیجه نقطه (3) در موقعیت بدتری نسبت به دو نقطه (1) (2) قرار دارد، بنابراین نقطه (3) جواب مغلوب است.

مقدار تابع هدف f(x) نقطه (1) کمتر از مقدار تابع هدف نقاط (2) است، از طرفی مقدار تابع هدف g(x) نقطه (1) کمتر از مقدار تابع هدف نقاط (2) است، در نتیجه نقاط (1) و (2) برتری نسبت به یکدیگر ندارند، بنابراین نقاط (1) و (2) جواب‌های نامغلوب هستند.

از آنجایی نقطا بهتری نسبت به نقاط (1) و (2) پیدا نشده است، پارتو فرانت پیدا شده توسط روش حل برابر مجموع نقاط (1) و (2) است.

انواع مسائل بهینه‌سازی

مسائل بهینه‌سازی دودویی، گسسته و پیوسته

بر اساس نوع متغیرهای مجهول، مسائل بهینه‌سازی را میتوان به سه دسته دودویی،  گسسته و پیوسته تقسیم کرد.

مسائل بهینه‌سازی دودویی به مسائلی اطلاق می‌شود که متغیرهای مجهول آن را بتوان در قالب یک رشته دودویی(Binary) ارائه کرد. برای مثال در صورتی که هدف انتخاب زیر مجموعه‌ای از میان مجموعه ای بزرگتر باشد، انتخاب عدم انتخاب هر عضو مجموعه می‌تواند به صورت صفر یا یک نشان داده شود در نتیجه هر راه حل کاندید، رشته ای دودویی به اندازه ابعاد مجموعه خواهد بود که اعداد صفر و یک در آن به ترتیب بیانگر عدم انتخاب و انتخاب آن عضو است.

مسائل بهینه‌سازی گسسته عموماً پیچیدگی‌های بیشتری در مدلسازی و تعیین مقادیر بهینه دارند. در مسائل بهینه‌سازی گسسته یا ترکیبی، متغیرهای مسئله به صورت گسسته تعریف می‌شود. در واقع مجموعه محدودی از راه حل‌های کاندید وجود دارد. ساختار راه حل‌ها با توجه به مسئله بهینه‌سازی می‌تواند مرتب‌سازی، مسیریابی در شبکه، انتساب و… باشد. برای مثال در کاربرد مسیریابی ترتیب عبور از موقعیت‌های ممکن برای کمینه‌سازی طول مسیر از مبدا به مقصد مورد پرسش است. از این رو راه حل کاندیدی شامل ترتیب موقعیت ها برای عبور است.

 مسائل بهینه‌سازی پیوسته، متغیرهای مجهول در آنها از نوع اعداد حقیقی هستند. برای نمونه توابع ریاضی که نقاط کمینه یا بیشینه آن‌ها مورد سؤال است، جزء این دسته از مسائل قرار میگیرند. برای مثال مسئله کمینه‌سازی تابع رستریجین، مسئله بهینه‌سازی پیوسته‌ای است که راه حل کاندید آن شامل یک متغیر یا مقادیر پیوسته در بازه [۵.۱۲,۵.۱۲-] است.

برخی مسائل وجود دارد که به صورت همزمان دارای متغیرهایی با انواع مختلف گسسته و پیوسته، دودویی و پیوسته، گسسته و دودویی است.

مسائل بهینه سازی مقید و بدون قید

یکی از مؤلفه هایی که مسائل بهینه سازی را از یکدیگر متمایز می کند وجود یا عدم وجود قید (محدودیت) در آنهاست. در بسیاری از مسائل مجموعه ای از قیود (محدودیت‌ها) وجود دارد که لازم است متغیرها در آنها صدق کند تا نتایج معنادار باشند. در بسیاری از کاربردهای عملی، محدودیت‌هایی در مقدار متغیرهای مسئله وجود دارد که به صورت قید (محدودیت) به مسئله بهینه‌سازی اضافه می‌شود. قیود به روش‌های مختلف فرموله می‌شوند؛ مانند قیود مساوی، نامساوی، ارتباط بین متغیرها و… 

در مثال زیر، هدف کمینه‌سازی مقید تابع هدف f با n متغیر است که قید مساوی g و قیود نامساوی h و k نیز به مسئله اضافه شده است. با توجه به روش حل می‌توان این مسئله مقید را به صورت مقید یا با استفاده از تبدیل آن به مسئله نامقید حل کرد.

مسئله بهینه‌سازی قطعی و غیر قطعی

در مسائل بهینه‌سازی قطعی فرض می‌شود داده ورودی مسئله کاملاً معلوم و تعریف شده است.

هر چند در بسیاری از کاربردها به دلیل وجود خطاهای اندازه گیری و همچنین وجود داده های پیش‌بینی، عدم قطعیت در دقت داده‌ها وجود دارد. عدم قطعیت موجود در داده عموماً در مدل ریاضی در نظر گرفته می‌شود. برای نمونه در برخی از کاربردهای مهندسی اندازه گیری یک کمیت چندین بار انجام میشود و در نهایت دقت اندازه گیری آن محاسبه و متناسب با دقت وارد مسئله بهینه سازی میشود از سوی دیگر در برخی کاربردها نظیر تعیین موقعیت کمینه یک تابع ریاضی متغیرها به عنوان کمیتی قطعی وارد محاسبات میشوند.

مسائل بهینه‌سازی غیر قطعی که داده ورودی مسئله را قطعی در نظر نمی‌گیرند و به آن ماهیت عدم قطعیت می‌یخشند؛ عمدتاً به صورت آماری یا فازی تعریف می‌شوند. در  مسائل غیر قطعی آماری، متغیرها از توزیع‌های آماری مانند توزیع آماری پواسون، یکنواخت، برنولی و… استفاده می‌کنند. همانطور که گفته شد، نوع دیگر مسائل غیر قطعی مسائل فازی هستند. این مسائل متغیرهای عدم قطعیت را به صورت اعداد فازی مثلثی، ذوزنقه‌ای، LR و… استفاده می‌کنند. برای حل آن از روش‌های آماری مختلف به‌منظور رباست‌سازی مدل ریاضی یا متغیر غیر قطعی است.

این نکته حائل اهمیت است که یکی از راه‌های ساده و سریع برای انتخاب موضوع پرپوزال یا پایان‌نامه یا مقالات علمی داخلی و خارجی، تبدیل مسائل قطعی تغریف شده از قبل به مسائل غیر قطعی و حل آن است!

مسائل بهینه‌سازی با یک موقعیت بهینه و چندگانه

در بعضی از مسائل بهینه‌سازی، تابع هدف یک بهینه سراسری دارد. در این دسته از مسائل از روش‌های حل مختلف به منظور تعیین نقطه بهینه مطلق استفاده می‌شود. از سوی دیگر در مسائل بهینه‌سازی با چند موقعیت بهینه، باید مجموعه‌ای از موقعیت‌هایی که در تمامی آن‌ها تابع هدف بهینه است، تعیین شود. به مجموعه‌ای از این نقاط بهینه که همگی همزان نقاط بهینه مطلق مسئله هستند، پارتو فرانت (Pareto Front) میگویند.

مسائل بهینه‌سازی چندهدفه

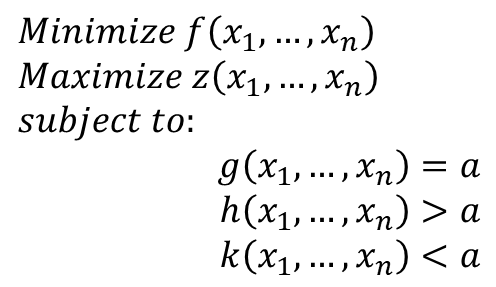
در مثال بالا، هدف کمینه‌سازی تابع هدف f با n متغیر و بیشینه‌سازی تابع هدف z با m متغیر است که قید مساوی g و قیود نامساوی h و k نیز به مسئله اضافه شده است. با توجه به روش حل، ساده‌ترین کار تبدیل این مسئله چند هدفه را به یک مسئله تک‌هدفه و حل آن است.

برنامه‌ریزی تسهیلات

مسائل برنامه‌ریزی تسهیلات به چهار دسته عمده مکان‌یابی، مسیریابی، تخصیص و طراحی تقسیم می‌شوند.

مسائل مکانیابی تسهیلات به تعیین مکان یک تسهیل (ساختمان، دستگاه، وسیله و…) جدید نست به یک تعداد وسیله موجود می‌پردازد. مکانی که به دنبال آن هستیم، جایی است که یک تابع هزینه کل تعریف‌شده را حداقل می‌کند و هزینه کل مذکور متناسب با فاصله در نظر گرفته می‌شود. مسائل تک‌هدفه مکانیابی در ساده‌ترین شکل ممکن به صورت زیر فرمول‌بندی می‌شوند:

m وسیله موجود در نقاط مشخص P ، قرار گرفته‌اند. یک تهسیل جدید قرار است در نقطه x قرار بگیرد. هزینه حمل و نقل مستقیماً متناسب با فاصله بین تهسیل جدید و موجود در نظر گرفته میشود. (x,p)d فاصله پیموده شده در هر سفر بین نقاط P و X و W ضرب هزینه هر واحد فاصله پیموده‌شده در تعداد سفرهای سالیانه بین تسهیل جدید و موجود را نشان میدهد. هزینه کل سالیانه سفر بین تسهیل جدید و همه تسهیلات موجود به وسیله فرمول زیر بیان می شود.

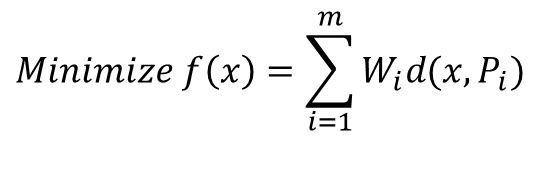
مسائل مسیر‌یابی تسهیلات شامل تعیین آرایش یا مسیر بهینه منابع، محصولات یا افراد است به گونه‌ای که هزینه‌ها کاهش یابد، بهره‌وری افزایش پیدا کند، یا اهداف خاص دیگری برآورده شود. این مسئله در حوزه‌های مختلفی مانند لجستیک، مدیریت زنجیره تأمین، مخابرات و برنامه‌ریزی شهری ظاهر می‌شود. توابع هدف این مسائل را می‌توان به صورت حداقل کردن هزینه‌های حمل‌ونقل یا عملیاتی، حداکثر کردن سطح خدمات یا پوشش، متعادل کردن استفاده از منابع در و… و محدودیت‌های این مسئله را می‌توان به‌صورت محدودیت‌های ظرفیت تسهیلات یا مسیرها، زمان‌بندی مشخص برای تحویل یا عملیات، محدودیت‌های جغرافیایی یا لجستیکی تعریف کرد. از مسائل معروف مسیریابی تسهیلات می‌توان به مسئله مسیر‌یابی وسایل نقلیه و مسئله طراحی شبکه اشاره کرد.

مسائل تخصیص تسهیلات  نوعی مسئله بهینه‌سازی است که در آن هدف، تخصیص منابع، خدمات یا مشتریان به تسهیلات مشخص به گونه‌ای است که یک هدف خاص بهینه شود. این مسئله اغلب در لجستیک، مدیریت زنجیره تأمین و برنامه‌ریزی شهری مطرح می‌شود و تصمیم‌گیری در مورد نحوه تخصیص تقاضا یا منابع به تسهیلات موجود برای افزایش بهره‌وری و کاهش هزینه‌ها اهمیت دارد.

مسائل طراحی تسهیلات به سه بخش چیدمان واحدهای صنعتی، تحلیل فرآیند جریان مواد و طراحی ساختار تقسیم می‌شوند.

مسائل چیدمان واحدهای صنعتی به تعیین محل و ترتیب قرارگیری تجهیزات، ماشین‌آلات، ایستگاه‌های کاری، و دیگر بخش‌های عملیاتی در داخل یک تسهیل یا کارخانه است، می‌پردازد. هدف از چیدمان بهینه، کاهش زمان و هزینه‌های جابه‌جایی مواد، افزایش بهره‌وری، و بهبود جریان کاری است.

یکی از معروف‌ترین مسائل طراحی تسهیلات، چیدمان واحدهای صنعتی است که تشابهاتی با مسئله مکانیابی تسهیلات دارد. در مسائل چیدمان علوه‌بر ضریب هزینه هر واحد جابه‌جایی W، ضریب جریان مواد و تعداد سفرهای مورد نیاز را نیز در نظر گرفت.

با این حال، مسائل مکانیابی و چیدمان تهسیلات تفاوت‌هایی دارند که عبارت‌اند از:
• چدیمان به معنای جانمایی، طرح استقرار و Layout است.
• مکانیابی به معنای جایابی و Location  است.
• مکان‌یابی یک هدف بلندمدت‌تر و استراتژیک‌تر نسبت به چیدمان است.
• ابتدا مکان‌ یک تهسیل مشخص شده و سپس آن را در محل مناسب آن قرار می‌دهند.

مسائل تحلیل فرآیند جریان مواد بر بررسی و تجزیه‌وتحلیل جریان مواد، قطعات، یا محصولات بین بخش‌های مختلف در یک تسهیل متمرکز است. هدف اصلی، به حداقل رساندن زمان حمل‌ونقل، کاهش هزینه‌ها، و کاهش نقاط گلوگاهی  در فرآیند تولید است.

مسائل طراحی ساختار شامل طراحی زیرساخت‌های فیزیکی و معماری تسهیلات است، از جمله ساختمان‌ها، انبارها، و سیستم‌های پشتیبانی. هدف این است که ساختاری ایجاد شود که بتواند نیازهای عملیاتی را برآورده کند و از توسعه‌های آینده پشتیبانی کند.

زمانبندی

زمان‌بندی یک فرآیند تصمیم‌گیری است که به طور منظم در بسیاری از صنایع تولیدی و خدماتی مورد استفاده قرار می‌گیرد. این فرآیند به تخصیص منابع به وظایف در بازه‌های زمانی مشخص می‌پردازد و هدف آن بهینه‌سازی یک یا چند هدف است.

منابع و وظایف در یک سازمان می‌توانند اشکال مختلفی داشته باشند. منابع ممکن است شامل ماشین‌آلات در یک کارگاه، باندهای فرود در یک فرودگاه، گروه‌های کاری در یک سایت ساخت‌وساز، واحدهای پردازشی در یک محیط محاسباتی و موارد مشابه باشند. وظایف نیز ممکن است شامل عملیات در یک فرآیند تولید، برخاستن و فرود هواپیماها در یک فرودگاه، مراحل یک پروژه ساختمانی، اجرای برنامه‌های کامپیوتری و موارد دیگر باشند. هر وظیفه ممکن است دارای سطح اولویت خاص، زمان شروع زودترین ممکن و مهلت نهایی باشد.

اهداف در زمان‌بندی نیز می‌توانند اشکال گوناگونی داشته باشند. یکی از اهداف ممکن است حداقل کردن زمان تکمیل آخرین وظیفه باشد و هدف دیگر ممکن است حداقل کردن تعداد وظایفی باشد که پس از مهلت نهایی خود تکمیل می‌شوند.

زمان‌بندی به عنوان یک فرآیند تصمیم‌گیری نقش مهمی در اکثر سیستم‌های تولیدی و ساخت‌و‌ساز و همچنین در بسیاری از محیط‌های پردازش اطلاعات ایفا می‌کند. این فرآیند در تنظیمات حمل‌ونقل و توزیع و در انواع دیگر صنایع خدماتی نیز اهمیت دارد. مثال‌های زیر نقش زمان‌بندی را در تعدادی از محیط‌های واقعی نشان می‌دهند.

لجستیک

لجستیک به فرآیند برنامه‌ریزی، اجرا، و کنترل جریان کارآمد و مؤثر کالاها، خدمات و اطلاعات از نقطه مبدأ تا مقصد نهایی برای برآورده کردن نیازهای مشتریان اشاره دارد. این مفهوم شامل هماهنگی میان منابع، حمل‌ونقل، انبارداری، و مدیریت اطلاعات است و نقش حیاتی در زنجیره تأمین و صنایع مختلف ایفا می‌کند.

از مهمترین مسائل لجستیک می‌توان کنترل موجودی، مدیریت حمل‌ونقل و زنجیره تأمین را نام برد.

کنترل موجودی عبارت است از فن نگهداری موجودی اقلام در سطح مطلوب به منظور برآوردن تقاضای مشتریان به میزان مناسب و در موعد مقرر به‌طوری که هزینه سیستم حداقل شود. هدف اصلی کنترل موجودی، تأمین نیازهای مشتریان یا فرآیندهای تولیدی با کمترین هزینه ممکن و به حداقل رساندن ریسک کمبود یا مازاد کالا است.

مدیریت حمل‌و‌نقل بخشی حیاتی از لجستیک و زنجیره تأمین است که بر برنامه‌ریزی، اجرا، نظارت و بهینه‌سازی جابه‌جایی کالاها، افراد یا اطلاعات بین نقاط مبدأ و مقصد تمرکز دارد. این فرآیند شامل انتخاب روش حمل‌ونقل، مسیرهای مناسب، نظارت بر عملیات حمل‌ونقل و مدیریت هزینه‌های حمل‌ونقل با استفاده از شناسایی و انتخاب مسیرهای کوتاه‌تر، حل مسئله فروسنده دوره‌گرد ( TSP ) و… می‌شود.

مدیریت زنجیره تأمین مجموعه‌ای از فرآیندها و فعالیت‌هایی است که با هماهنگی میان تامین‌کنندگان، تولیدکنندگان، توزیع‌کنندگان، و مشتریان، به مدیریت جریان مواد، اطلاعات، و منابع مالی در سراسر زنجیره تأمین می‌پردازد. هدف این مدیریت، افزایش کارایی، کاهش هزینه‌ها، و بهبود رضایت مشتریان از طریق ایجاد زنجیره‌ای هماهنگ و بهینه است.

حل سنتی مسائل چندهدفه

روش‌های حل سنتی تکنیک‌هایی در حل مسائل ریاضی و بهینه‌سازی هستند که مسائل چندهدفه را به مسائل تک‌هدفه تبدیل می‌کنند.

این روش جزء اولین روش‌های ارائه‌شده برای حل مسائل چندهدفه است.  هدف روش‌های حل سنتی، ساده‌سازی مسئله است. بدین جهت این روش‌ها به طور مستقیم قادر به یافتن پارتو فرانت مسئله نیستند و برای یافتن پارتو فرانت مسئله باید مسئله‌ی مورد نظر را در تنظیم‌های مختلف روش‌های سنتی حل کرد تا از مجموع آن جواب‌ها، پراتوفرانت مسئله را تشخیص داد؛ از طرفی این روش به‌دلیل کاهش ابعاد مسئله (تبدیل چندین تابع هدف به یک تابع هدف واحد)، قادر با یافتن بسیاری از جواب‌های بهینه نیستند!

بنابر ماهیت و اهداف مسئله می‌توان از روش‌های حل سنتی از جمله جمع وزنی، محدودیت اپسیلون، برنامه‌ریزی آرمانی، سلسله‌مراتبی، محالحه، توابع جریمه، تابع مجازات داخلی، عملکرد جریمه بیرونی، ضریب لاگرانژ، مجازت اعدام اشاره کرد.

حل مدرن مسائل چندهدفه

روش‌های حل مدرن به تکنیک‌هایی اطلاق می‌شود که برای حل مسائل پیچیده و بهینه‌سازی، مجموعه راه‌حل‌هایی نزدیک به پارتو فرانت ارائه می‌دهند. روش‌های مدرن اغلب راه‌حل‌هایی با دقت قابل قبول و زمان حل کوتاه ارائه می‌دهند.

روش‌های حل مدرن به دو دسته ابتکاری و فراابتکاری تقسیم می‌شوند.

روش‌های ابتکاری

روش‌های جست‌و‌جوی ابتکاری عمدتاً بر مبنای روش‌های شمارشی هستند، با این تفاوت که از اطلاعات دیگری به منظور هدایت جست‌وجو و کاهش زمان و حجم محاسبات استفاده میکنند. این دسته از روش‌ها ضمانتی برای تعیین نقاط بهینه مطلق در فضای جست‌و‌جو ارائه نمی دهند، بلکه پاسخی مطلوب نزدیک به بهینه در زمانی محدود برای یک مسئله بهینه‌سازی با پیچیدگی‌های زیاد ارائه می‌کنند. روش‌های جست‌و‌جوی ابتکاری را می‌توان به چهار دسته آزاد، تجزیه، سازنده و جست‌و‌جوی بهبود یافته تقسیم کرد.

روشهای فراابتکاری

الگوریتم‌های ابتکاری در مسائل پیچیده دچار مشکل می‌شوند و بهینه نسبی را به‌عنوان پاسخ نهایی معرفی می‌کنند. الگوریتم‌های جست‌و‌جوی فراابتکاری با هدف بهبود نتایج الگوریتم‌های ابتکاری ارائه شده‌اند. در این دسته از روش‌ها، تکنیک‌هایی به منظور رها شدن از بهینه‌های نسبی ارائه شده‌اند و همچنین به دلیل انعطاف‌پذیری زیاد، امکان استفاده از آن‌ها در بسیاری از مسائل بهینه‌سازی در علوم مختلف فراهم است. الگوریتم‌های فراابتکاری روشی تقریبی هستند.

همچنین الگوریتم‌های فراابتکاری مختص مسائل خاصی نیستند و با توجه به قابلیت انعطاف‌پذیری زیاد، امکان به‌کارگیری آن‌ها در مسائل بهینه‌سازی مختلف با انواع متغيرها، وجود یا عدم وجود قید، یک یا چند تابع هدف وجود دارد. به عبارت دیگر الگوریتم‌های فراابتکاری تکنیک‌هایی عمومی هستند که با کمی تغییر می‌توانند در حل بیشتر مسائل بهینه‌سازی به کار بروند.

دو مؤلفه اصلی الگوریتم‌های فراابتکاری جست و جوی محلی و جست و جوی سراسری هستند که استفاده همزمان از این دو موجب بهبود عملکرد جست وجو می‌شود. در نظر گرفتن جست و جوی محلی پیرامون مناطق با کیفیت کشف شده می‌تواند در رسیدن به جواب‌های بهینه الگوریتم را هدایت کند و در طرف مقابل توانایی جست و جوی سراسری با ماهیت تصادفی بودن الگوریتم امکان جلوگیری از رسیدن به بهینه‌های محلی را فراهم می‌کند. در صورتی که ترکیبی مناسب از این دو قابلیت فراهم شود. احتمال کشف جواب بهینه در الگوریتم‌های بهینه‌سازی فراابتکاری افزایش می یابد.

بنابر نوع مسئله و اهمیت زمان یا کیفیت حل انواع الگوربتم‌های فراابتکاری را می‌توان انتخاب و استفاده کرد. الگوریتم‌های فراابتکاری چندهدفه با استفاده از ایجاد تغییراتی در الگوریتم‌های فراابتکاری تک‌هدفه ایجاد شده اند.